

發布時間:所屬分類:工程師職稱論文瀏覽:1次
摘 要: 摘要:軌道車輛零碳感知技術在零碳排放的前提下實現軌道車輛狀態感知及數據互聯,有助于推進碳中和及智慧地鐵發展,保障軌道車輛綠色安全運營。壓電俘能結構可為軌道車輛零碳感知傳感提供能源,是零碳感知的核心部件。常規的懸臂梁式壓電俘能結構在受到激烈沖擊時易造
摘要:軌道車輛零碳感知技術在零碳排放的前提下實現軌道車輛狀態感知及數據互聯,有助于推進碳中和及智慧地鐵發展,保障軌道車輛綠色安全運營。壓電俘能結構可為軌道車輛零碳感知傳感提供能源,是零碳感知的核心部件。常規的懸臂梁式壓電俘能結構在受到激烈沖擊時易造成壓電陶瓷碎裂,難以滿足軌道車輛零碳感知需求且缺乏統一有效的工程化建模方法阻礙了零碳感知技術應用。為了實現軌道車輛零碳傳感自驅動,設計一種新型的雙端固支式壓電梁俘能結構,并針對該結構提出一種非線性車輛振動下的統一工程化建模及發電特性分析方法。通過數值計算、仿真分析及實驗測試驗證方法的準確性。研究結果表明,工程模型能夠準確表征實際壓電梁發電特性,在無量綱壓電負載一定時無量綱平方壓電力壓轉換因子越大輸出功率也越大,機械品質因子不影響輸出功率其大小決定了響應頻率的選擇性強弱械品質因子越大選擇性越強,當無量綱平方壓電力壓轉換因子與機械品質因子一定的情況下頻率比值為 1 與無量綱壓電負載為 0.8 時輸出性能達到最佳。理論計算值與仿真值及實測值之間的最大絕對功率偏差分別為 0.036mW 和 0.029mW,相對偏差百分比為 2.501%與 2.154%;最大絕對峰值電壓偏差為 0.067V 和 0.055V,相對偏差百分比為 1.243%與 1.035%,可為軌道車輛零碳感知技術推廣與應用提供理論基礎。
關鍵詞:軌道車輛;零碳感知;壓電俘能;工程模型;發電特性
軌道車輛零碳感知兼顧綠色環保及軌道車輛狀態數據感知互聯,其技術的發展有助于碳達峰及碳中和目標的實現、推進交通強國倡議中數據資源賦能交通的發展。利用壓電發電實現軌道車輛狀態感知傳感器自驅化是軌道車輛零碳感知的核心技術[1-3]。壓電俘能結構建模及發電特性分析[4]是實現軌道車輛傳感設備能源自供給的理論基礎。壓電俘能器通常采用壓電懸臂梁結構[5-7],該結構一端固定一端自由運動 [8-9],一般主要是由壓電陶瓷、金屬基底和質量塊組成[10-11],壓電陶瓷受外界作用力下發生形變,從而引起正壓電效應產生電荷。然而,受輪軌作用力及線路不平順的影響,軌道車輛走行部處的瞬間沖擊高達 100g 以上[12],常規懸臂梁式壓電俘能結構通常應用在 1g 以下[3],造成壓電陶瓷碎裂而較難滿足軌道車輛走行部處微傳感器供電需求。針對壓電懸臂梁建模及發電特性分析上,以往的建模方法通常是基于壓電梁結構及力學特征建立其分布參數機電耦合模型[13-17],這會導致模型公式復雜、參數繁多,不利于模型求解和工程化應用。思建行等[13]通過分析壓電梁機電耦合特性并利用模態分析法構建了雙晶片壓電懸臂梁雙向耦合分布參數模型;郭抗炕等[14]在考慮壓電材料非線性特性基礎上建立了單晶壓電懸臂梁機電耦合模型,獲得了壓電材料非線性、外激勵參數及負載電阻對發電功率的影響規律;孫舒等[17]針對雙穩態壓電懸臂梁發電系統建立了集中參數模型并得到了其懸臂梁發電系統的特性。因此,目前軌道車輛零碳技術中壓電俘能發電難點在于缺少適應軌道車輛振動強烈且瞬間沖擊大的俘能結構和統一的工程化建模手段及方法,以達到與車輛振動頻率適配及功率最大化發電目的。針對該問題,本文采用一種新型壓電俘能結構,并針對該結構提出了一種統一的工程化建模方法,實現了發電特性工程化分析,可為軌道車輛零碳感知技術推廣與應用提供理論基礎。
1 軌道車輛零碳感知壓電俘能工程建模
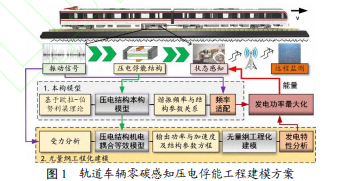
軌道車輛零碳感知壓電俘能結構工程建模是實現軌道車輛走行部件健康狀態零碳排放感知及數據互聯互通的傳感設備能源自供給的理論基礎。圖 1 給出了軌道車輛零碳感知壓電俘能工程建模方案,首先,基于歐拉-伯努利梁理論建立雙端固支式壓電懸臂梁本構模型,推導出壓電俘能結構諧振頻率與結構參數關系,可為頻率適配提供理論基礎;其次,對非線性車輛振動狀態下壓電俘能結構進行受力分析,獲取壓電結構機電耦合等效模型,得到輸出功率與加速度及結構參數方程,并通過構建無量綱工程化模型簡化方程的復雜程度,可實現發電特性工程化分析及應用。
1.1 壓電俘能結構及本構模型
為了適應軌道車輛振動強烈且瞬間沖擊較大[18-20]的實際應用環境,采用新型雙端固支式壓電梁結構如圖 2 所示,該結構是由金屬基底、壓電陶瓷及質量塊組成。壓電陶瓷粘貼于金屬基底的上下表面組成壓電雙晶片,質量塊通過螺栓固定于雙晶片上下壓電陶瓷表面中央處,雙晶片兩端固定,當壓電梁受到外界振動時,質量塊由于慣性作用使雙晶片發生機械形變,從而將機械能轉換為電能。
1.2 無量綱工程化建模
在軌道車輛運行過程中,壓電梁主要受到輪軌垂向連續加速度及瞬間沖擊所引起的作用力影響,分別為輪軌垂向加速度及沖擊作用下質量塊慣性力和因壓電梁響應加速度與固定支點激勵加速度不同產生的相對作用力。將質量塊慣性力等效為 F(t),支點相對作用力產生的位移為 y(t),壓電梁等效為剛度為𝑘𝑠和阻尼系數為𝑏𝑡的彈簧阻尼系統的等效機械模型和電流源與壓電等效夾持電容𝐶𝑝并聯的等效電路模型,則壓電結構機電耦合等效模型如圖 4 所示。
2 模型驗證及發電特性分析
為了驗證軌道車輛零碳感知壓電俘能無量綱工程化建模方法正確性,以獲取軌道車輛零碳感知用壓電俘能結構發電特性。利用 COMSOL 有限元軟件構建了雙端固支式壓電梁仿真模型如圖 5 所示,該模型主要包括金屬基底、上下壓電陶瓷片及質量塊組成,其關鍵參數如表 2 所示,仿真模型采用自由四面體網格劃分方式。通過對上海地鐵 5 號線阿爾斯通車輛的軸箱處振動加速度進行采集,采樣頻率為 5kHz,測試區間為劍川路測試線,并通過傅里葉變換分析獲取了軌道車輛振動加速度一階主頻率為 83Hz。因此,仿真設定激勵加速度頻率范圍為 82 到 84Hz 之間的正弦信號,以步長為 0.2Hz 進行掃頻。
圖 6 為搭建的實驗平臺,主要包括主機、信號發生器、功率放大器、激振器、壓電陶瓷、轉換電路、控制軟件和示波器組成,采用與仿真模型相同的參數及激勵大小。
圖 9 和圖 10 分別為對應頻率從 82Hz 到 84Hz 時輸出功率絕對偏差和峰值電壓絕對偏差對比曲線。表 3 為頻率從 82Hz 到 84Hz 之間的輸出功率及峰值電壓統計結果。從圖 9、圖 10 和表 3 中可以看出,理論值與仿真值之間的輸出功率絕對偏差和絕對峰值電壓偏差均較小,最大偏差為 82.8Hz 下,其對應的理論輸出功率𝑃為 1.446mW,理論峰值電壓𝑉𝑝為 5.378V;仿真輸出功率𝑃為 1.482mW,仿真峰值電壓𝑉𝑝為 5.445V。對應的最大絕對功率偏差𝑀𝐴𝐸𝑃為 0.036mW,功率相對偏差百分比𝐸𝑃為 2.501%;最大絕對峰值電壓偏差𝑀𝐴𝐸𝑉𝑃為 0.067V,峰值電壓相對偏差百分比𝐸𝑉𝑃為 1.243%。同理,從圖 9、圖 10 和表 3 中也可以得出,理論值與實測值之間的輸出功率絕對偏差和絕對峰值電壓偏差均較小,最大偏差為 82.4Hz 加速度下,其對應的理論輸出功率𝑃為 1.383mW,理論峰值電壓𝑉𝑝為 5.259V;實測輸出功率𝑃為 1.412mW,仿真峰值電壓𝑉𝑝為 5.197V。對應的最大絕對功率偏差𝑀𝐴𝐸𝑃為 0.029mW,功率相對偏差百分比𝐸𝑃為 2.154%;最大絕對峰值電壓偏差𝑀𝐴𝐸𝑉𝑃為 0.055V,峰值電壓相對偏差百分比𝐸𝑉𝑃為 1.035%。
為了進一步分析壓電俘能結構在一階諧振頻率下模型精度,表 4 給出了在 83Hz 下理論值、仿真值與實測值所對應的輸出功率及峰值電壓的統計結果。從表 4 可以看出,在一階諧振頻率下理論輸出功率𝑃為 1.465mW,理論峰值電壓𝑉𝑝為 5.412V;仿真輸出功率𝑃為 1.500mW,仿真峰值電壓𝑉𝑝為 5.477V;實測輸出功率𝑃為 1.484mW,實測峰值電壓𝑉𝑝為 5.447V;對應的仿真最大絕對功率偏差𝑀𝐴𝐸𝑃為 0.035mW,功率相對偏差百分比𝐸𝑃為 2.390%;仿真最大絕對峰值電壓偏差𝑀𝐴𝐸𝑉𝑃為 0.065V,峰值電壓相對偏差百分比𝐸𝑉𝑃為 1.201%。同理,對應的實測最大絕對功率偏差𝑀𝐴𝐸𝑃為 0.019mW,功率相對偏差百分比𝐸𝑃為 1.297%;仿真最大絕對峰值電壓偏差𝑀𝐴𝐸𝑉𝑃為 0.035V,峰值電壓相對偏差百分比𝐸𝑉𝑃為 0.647%。對比仿真數據和實測數據可以得出,理論值在一階諧振頻率下,建立的無量綱工程化模型的計算值更加靠近實測值。
綜上所述,無量綱工程模型無論是在一階諧振頻率附近還是一階諧振頻率點處精度均在 3%以內,且理論計算值均比仿真值更加接近實測數值,這說明本文所建立的模型不僅在保障精度的前提下實現模型簡化,而且更能反映壓電懸臂梁實際輸出特性。
為了分析軌道車輛零碳感知用壓電俘能結構發電特性,利用無量綱工程模型分別研究了不同無量綱平方壓電力壓轉換因子下無量綱壓電負載與最大歸一化輸出功率關系,不同機械品質因子下頻率比與最大歸一化輸出功率關系和最大歸一化輸出功率隨頻率比和無量綱壓電負載變化關系。
圖 11 不同無量綱平方壓電力壓轉換因子下無量綱壓電負載與最大歸一化輸出功率關系曲線。圖 11 表明無量綱平方壓電力壓轉換因子的增大對壓電梁的最大歸一化輸出功率產生較大影響,且無量綱平方壓電力壓轉換因子值越大歸一化輸出功率也越大。歸一化輸出功率的隨著無量綱壓電負載的增大至最大值隨后逐步減小,存在最優無量綱壓電負載使得軌道車輛零碳感知壓電俘能輸出功率最大。
圖 12 為不同機械品質因子下頻率比與最大歸一化輸出功率關系曲線。從圖 12 可以看出,機械品質因子值的增加對壓電梁的最大歸一化輸出功率并無影響,而對頻率比帶寬有明顯的影響。機械品質因子值大小代表著壓電梁對激勵頻率選擇性的強弱,隨著機械品質因子值的增大,頻率選擇性越強。
圖 13 為最大歸一化輸出功率隨頻率比和無量綱壓電負載變化關系曲線。從圖 13 可以得出: 當頻率比值固定時,最大歸一化輸出功率隨無量綱壓電負載值的增大呈現出先增大后減小的趨勢,當達到 0.8 附近時趨近于極限值 1,輸出功率最大;同樣,當無量綱壓電負載值固定時,最大歸一化輸出功率隨頻率比值的增大呈現出先增大后減小的趨勢,當頻率比達到 1 附近時輸出功率趨近于極限值 1。因此,當無量綱平方壓電力壓轉換因子與機械品質因子一定的情況下,頻率比值為 1 與無量綱壓電負載為 0.8 時,軌道車輛零碳感知壓電俘能輸出性能達到最佳。
3 結論
1)無量綱平方壓電力壓轉換因子值越大歸一化輸出功率也越大。歸一化輸出功率的隨著無量綱壓電負載的增加呈現先增加后減小趨勢,且存在最優無量綱壓電負載使得輸出功率最大;
2)對于雙端固支式壓電梁結構,增大壓電懸臂梁的機械品質因子值,不會影響最大歸一化輸出功率,但是會減小其頻率比帶寬,即提高壓電梁的頻率選擇能力;
3)當壓電梁的機械品質因子值和無量綱平方壓電力壓轉換因子值固定時,最大歸一化輸出功率受到頻率比值和無量綱壓電負載共同作用影響,且在頻率比值為 1 與無量綱壓電負載為 0.8 時,壓電懸臂梁輸出性能達到最佳;
4)在諧振頻率處,理論計算值與仿真值及實測值之間的最大絕對功率偏差分別為 0.035mW 和 0.019mW 對應的相對偏差百分比為 2.390%與 1.297%;最大絕對峰值電壓偏差為 0.065V 和 0.035V 對應的相對偏差百分比為 1.201%與 0.647%。基于無量綱模型構建的壓電懸臂梁模型不僅在保障模型精度的前提下實現了模型簡化,而且更能反映壓電懸臂梁實際輸出特性。——論文作者:丁亞琦 1,彭樂樂 2,李曉靖 1,周炯 1,鄭樹彬 2,張園 2
參考文獻:
[1] HODGE V J, O'KEEFE S, WEEKS M, et al. Wireless sensor networks for condition monitoring in the railway industry: a survey[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(3): 1088-1106.
[2] ZHOU Wanlu, ZUO Lei. A self-powered piezoelectric vibration control system with switch precharged inductor (SPCI) method[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(2): 773-781.
[3] 亓有超,趙俊青,張弛.微納振動能量收集器研究現狀與展望[J]. 機械工程學報,2020,56(13):1-15. QI Youchao, ZHAO Junqing, ZHANG Chi. Review and prospect of micro-nan0 vibration energy harvesters[J]. Journal of Mechanical Engineering, 2020,56(13):1-15.
[4] SHI Ge, XIA Yinshui, YANG Yanmei, et al. A sensorless self-tuning resonance system for piezoelectric broadband vibration energy harvesting[J]. IEEE Transactions on Industrial Electronics, 2021, 68(3): 2225-2235.
[5] HU Guobiao, WANG Junlei, TANG Lihua. A comb-like beam based piezoelectric system for galloping energy harvesting[J]. Mechanical Systems and Signal Processing, 2021, 150: 107301.
[6] 蔣樹農,郭少華,李顯方.單壓電片懸臂梁式壓電俘能器效能分析[J].振動與沖擊,2012,31(19):90-94. JIANG Shunong, GUO Shaohua, LI Xianfang. Performance analysis for a unimorph cantilever piezoelectric harvester[J]. Journal of Vibration and Shock, 2012, 31(19): 90-94.
[7] 袁江波,謝濤,單小彪,等.復合型懸臂梁壓電振子振動模型及發電實驗研究[J]. 機械工程學報,2010,46(9):87-92. YUAN Jiangbo, XIE Tao, SHAN Xiaobiao, et al. Vibrated model and experiments of multiple piezoelectric cantilevers in energy harvesting[J]. Journal of Mechanical Engineering, 2010, 46(9): 87-92.
[8] SANG Yingjun, HUANG Xueliang, LIU Hexiang, et al. A vibration-based hybrid energy harvester for wireless sensor systems[J]. IEEE Transactions on Magnetics, 2012, 48(11): 4495-4498.
[9] GURJAR M, JALILI N. Toward ultrasmall mass detection using adaptive self-sensing piezoelectrically driven microcantilevers[J]. IEEE/ASME Transactions on Mechatronics, 2007, 12(6): 680-688.
[10] 馬小青,李帥波,王喃喃. 復合式壓電懸臂發電梁設計與實驗分析[J]. 儀表技術與傳感器,2019,16(10):8-11. MA Xiaoqing, LI Shuaibo, WANG Nannan. Design and experimental analysis of composite piezoelectric cantilever beeam [J]. Instrument Technique and Sensor, 2019, 16(10): 8-11.